domingo, 12 de mayo de 2013
viernes, 29 de marzo de 2013
FUNCIONES CUBICAS Y EJEMPLOS*
Función Cúbica. Es generalmente utilizada para relacionar volúmenes en determinados espacio o tiempo. Otro ejemplo es el relacionar el crecimiento de un feto en gestación con el hecho de relacionar su distancia de los pies a la cabeza se puede determinar la semanas de gestación del feto. También el hecho de relacionar los vientos o la energía eólica con respecto a la intensidad de estos y su tiempo de duración. Se utiliza más en el campo de la economía y de la física
WEB GRAFIA: http://www.ecured.cu/index.php/Archivo:Funcion-cubica.jpg
Ejemplos
Grafique y analice las propiedades de la siguientes funciones
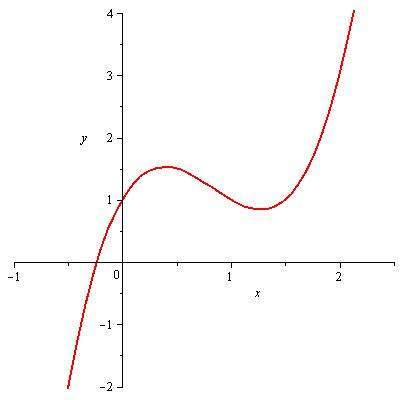
a) f(x) = 2x3 + 3x2 - 12x
Propiedades
2x3 + 3x2 - 12x = 0 x( 2x2 + 3x - 12) = 0 Extrayendo factor común x = 0 ( 2x2 + 3x + 12)= 0 Igualando a cero ambos factores y realizar la descomposición.
f(-1) = 2(-1)3 + 12 . (-1)2 + 2. (-1 )
b) F(x) = -x3 +8
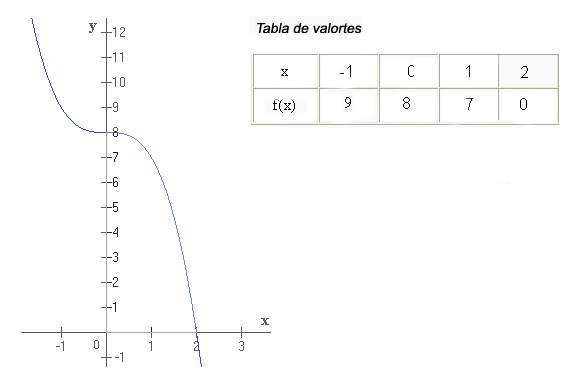
WEB GRAFIA: http://www.ecured.cu/index.php/Funci%C3%B3n_C%C3%BAbica

WEB GRAFIA: http://www.ecured.cu/index.php/Archivo:Funcion-cubica.jpg
Ejemplos
Grafique y analice las propiedades de la siguientes funciones
a) f(x) = 2x3 + 3x2 - 12x
Propiedades
- Dominio: El conjunto de los Reales
- Imagen: El conjunto de los Reales
- Ceros de la función:
2x3 + 3x2 - 12x = 0 x( 2x2 + 3x - 12) = 0 Extrayendo factor común x = 0 ( 2x2 + 3x + 12)= 0 Igualando a cero ambos factores y realizar la descomposición.
- Simetría: Demostrar que cumple f(-x)=-f(x).
f(-1) = 2(-1)3 + 12 . (-1)2 + 2. (-1 )
= 2.(-1) + 12 . 1 - 2
= -2 + 12 - 2
= 10 - 2
= 8
f(1) = 2(1)3 + 12 . (1)2 + 2. (1 ) = 2.(1) - 12 . 1 + 2
= 2 - 12 + 2
= -10 + 2
= -8
Como f(-1) = - f(1) por tanto la función es simétrica.- Continuidad: La función es continua en todo su dominio pues gráficamente se puede observar que no tiene ningún punto de discontinuidad.
- La función no tiene asuntotas.
- Para determinar los puntos donde la función corta el eje de la y
b) F(x) = -x3 +8

WEB GRAFIA: http://www.ecured.cu/index.php/Funci%C3%B3n_C%C3%BAbica
FUNCION CUADRATICA Y EJEMPLOS*
Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.
f(x) = ax² + bx +c
Representación gráfica de la parábola
Podemos construir una parábola a partir de estos puntos:
1. Vértice

Por el vértice pasa el eje de simetría de la parábola.
La ecuación del eje de simetría es:
2. Puntos de corte con el eje OX
En el eje de abscisas la segunda coordenada es cero, por lo que tendremos:
ax² + bx +c = 0
Resolviendo la ecuación podemos obtener:
Dos puntos de corte: (x1, 0) y (x2, 0) si b² − 4ac > 0
Un punto de corte: (x1, 0) si b² − 4ac = 0
Ningún punto de corte si b² − 4ac < 0
3. Punto de corte con el eje OY
En el eje de ordenadas la primera coordenada es cero, por lo que tendremos:
f(0) = a · 0² + b · 0 + c = c (0,c)
Representar la función f(x) = x² − 4x + 3.
1. Vértice
x v = − (−4) / 2 = 2 y v = 2² − 4· 2 + 3 = −1
V(2, −1)
2. Puntos de corte con el eje OX
x² − 4x + 3 = 0

(3, 0) (1, 0)
3. Punto de corte con el eje OY
(0, 3)

WEB GRAFIA: http://www.vitutor.com/fun/2/c_5.html
Ejercicios resueltos de la función cuadrática
1
Representa gráficamente la función cuadrática:
y = -x² + 4x - 3
1. Vértice
x v = - 4/ -2 = 2 y v = -2² + 4· 2 - 3 = -1 V(2, 1)
2. Puntos de corte con el eje OX.
x² - 4x + 3 = 0
 (3, 0) (1, 0)
(3, 0) (1, 0)
3. Punto de corte con el eje OY.
(0, -3)

WEB GRAFIA: http://www.vitutor.com/fun/2/e_c.html
FUNCION LINEAL Y EJEMPLOS*
La función lineal es del tipo:
y = mx + n
m es la pendiente de la recta.
La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Dos rectas paralelas tienen la misma pendiente.

n es la ordenada en el origen y nos indica el punto de corte de la recta con el eje de ordenadas.

WEB GRAFIA: http://www.vitutor.net/1/funcion_lineal.html
miércoles, 20 de febrero de 2013
lunes, 18 de febrero de 2013
sábado, 9 de febrero de 2013
INTERVALOS E INECUACIONES LINEALES
Intervalos e inecuaciones lineales
1.
Intervalos e inecuaciones lineales
Los intervalos son subconjuntos de los números reales que se pueden representar gráficamente en la recta numérica por un trazo o una semirrecta.
Los intervalos son subconjuntos de los números reales que se pueden representar gráficamente en la recta numérica por un trazo o una semirrecta.
Existen
intervalos abiertos, en los que no se incluyen los extremos; cerrados
en los que se
incluyen los extremos, y por último aquellos en que se combinan ambos.
Para representarlos se utiliza una circunferencia vacía en el extremo, si este no se incluye, o rellena si se incluye.
incluyen los extremos, y por último aquellos en que se combinan ambos.
Para representarlos se utiliza una circunferencia vacía en el extremo, si este no se incluye, o rellena si se incluye.
La
simbología que se utiliza en los casos abiertos (que no incluyen al extremo)
son el signo < o >; y para los casos cerrados (que incluyen al extremo)
son el signo
(mayor
o igual, o menor o igual).
Por
otra parte, los intervalos se pueden representar en forma de conjunto o con
corchetes:
Ejemplo:
Todos
los reales comprendidos entre a
y b, sin incluir a,
ni b.
Todos
los reales mayores que a, sin incluir a.
Todos
los reales entre m y n,
incluyendo a m y no incluyendo a n.
Ejemplo:
Observa
el esquema:
miércoles, 6 de febrero de 2013
EJEMPLOS DEDESIGUALDADES
EJEMPLOS DE DESIGUALDADES::




Criterios de equivalencia de inecuaciones
Si a los dos miembros de una inecuación se les suma o se les resta un mismo número, la inecuación resultante es equivalente a la dada.
La solución de una inecuación es el conjunto
de valores de la variable que verifica la inecuacíón.
Podemos
expresar la solución de la inecuación mediante:
1. Una representación gráfica.
2. Un intervalo.
2x − 1
< 7
2x < 8 x < 4
(-∞, 4)
2x − 1 ≤ 7
2x ≤ 8 x ≤ 4
(-∞, 4]
2x − 1
> 7
2x > 8 x > 4

(4, ∞)
2x − 1 ≥ 7
2x ≥ 8 x ≥ 4

Criterios de equivalencia de inecuaciones
Si a los dos miembros de una inecuación se les suma o se les resta un mismo número, la inecuación resultante es equivalente a la dada.
3x + 4
< 5 3x
+ 4 − 4 < 5 − 4 3x
< 1
Si a los dos miembros de una inecuación se
les multiplica o divide por un mismo número positivo, la inecuación resultante es equivalente a la dada.
2x < 6
2x : 2 < 6 : 2 x
< 3
Si a los dos miembros de una inecuación se
les multiplica o divide por un mismo número negativo, la inecuación resultante cambia de sentido y es equivalente a la dada.
−x < 5
(−x) · (−1) > 5 · (−1) x > −5
DESIGUALDADES

DESIGUALDADES O INECUACIONES:
Una inecuación es una desigualdad
algebraica en la que sus
dos miembros aparecen ligados por uno de estos signos:
|
<
|
menor que
|
2x − 1 < 7
|
|
≤
|
menor o igual que
|
2x − 1 ≤ 7
|
|
>
|
mayor que
|
2x − 1 > 7
|
|
≥
|
mayor o igual que
|
2x − 1 ≥ 7
|
Inecuaciones equivalentes
Si a los dos miembros de una
inecuación se les suma o se les resta un mismo número, la inecuación resultante es
equivalente a la dada.
Si a los dos miembros de una
inecuación se les multiplica o divide por un mismo número positivo, la inecuación resultante es
equivalente a la dada.
Si a los dos miembros de una
inecuación se les multiplica o divide por un mismo número negativo, la inecuación resultante cambia de sentido y es equivalente a la dada.
Resolución de inecuaciones de
primer grado
1º Quitar paréntesis.
2º Quitar denominadores.
3º Agrupar los términos en x a
un lado de la desigualdad y los términos independientes en el otro.
4º Efectuar las operaciones
5º Como el coeficiente de
la x es negativo multiplicamos por −1, por lo que cambiará el sentido de la
desigualdad.
6º Despejamos la incógnita.
Obtenemos la solución como una
desigualdad, pero ésta también podemos expresarla:
De forma gráfica
Como un intervalo
Resolución de sistemas de
inecuaciones con una incógnita
Se resuelve cada inecuación por
separado, siendo el conjunto solución del sistema la intersección de los
conjuntos soluciones de ambas inecuaciones.
WEB GRAFIA: http://www.vitutor.com/ecuaciones/ine/res.html
jueves, 31 de enero de 2013
lunes, 28 de enero de 2013
EXPONENTES(POTENCIAS) Y LOGARITMOS*
Definición
de logaritmo
De la definición de logaritmo podemos deducir:
No existe el logaritmo de un número con base negativa.
No existe el logaritmo de un número negativo.
No existe el logaritmo de cero.
El logaritmo de 1 es cero.
El logaritmo en base a de a es uno.
El logaritmo en base a de una potencia en base a es igual al exponente.
Propiedades
de los logaritmos
1El logaritmo de un producto es igual a la suma de los
logaritmos de los factores.
2 El logaritmo de un cociente es igual al logaritmo del
dividendo menos el logaritmo del divisor.
3El logaritmo de una potencia es igual al producto del
exponente por el logaritmo de la base.
4El logaritmo de una raíz es igual al cociente entre el
logaritmo del radicando y el índice de la raíz.
5Cambio de base:
WEN GRAFIA LINK: http://www.vitutor.com/fun/2/c_14.html
Potencias
Una
potencia es una forma abreviada de escribir un producto formado por varios
factores iguales.
6 · 6 · 6 · 6 · 6 = 65
Los
elementos que constituyen una potencia son:
La
base de la potencia es el número que multiplicamos por sí mismo, en este caso
el 6.
El
exponente de una potencia indica el número de veces que multiplicamos la base,
en el ejemplo es el 5.
Propiedades
de las potencias de números naturales
1 Un número elevado a 0 es igual a 1
Ejemplo:
50
= 1
2 Un número elevado a 1 es igual a sí mismo
Ejemplo:
51
= 5
3 Producto de potencias con la misma base
Es
otra potencia con la misma base y cuyo exponente es la suma de los exponentes.
Ejemplo:
25
· 22 = 25+2 = 27
4 División de potencias con la misma base
Es
otra potencia con la misma base y cuyo exponente es la diferencia de los
exponentes.
Ejemplo:
25
: 22 = 25 − 2 = 23
5 Potencia de una potencia
Es
otra potencia con la misma base y cuyo exponente es el producto de los
exponentes.
Ejemplo:
(25)3
= 215
6 Producto de potencias con el mismo exponente
Es
otra potencia con el mismo exponente y cuya base es el producto de las bases.
Ejemplo:
23
· 43 = (2 · 4)3=83
7 Cociente de potencias con el mismo exponente
Es
otra potencia con el mismo exponente y cuya base es el cociente de las bases.
Ejemplo:
63
: 33 = (6:2)3=23
WEB GRAFIA LINK: http://www.vitutor.com/di/n/a_6.html
Suscribirse a:
Comentarios (Atom)



















