viernes, 29 de marzo de 2013
FUNCIONES CUBICAS Y EJEMPLOS*
Función Cúbica. Es generalmente utilizada para relacionar volúmenes en determinados espacio o tiempo. Otro ejemplo es el relacionar el crecimiento de un feto en gestación con el hecho de relacionar su distancia de los pies a la cabeza se puede determinar la semanas de gestación del feto. También el hecho de relacionar los vientos o la energía eólica con respecto a la intensidad de estos y su tiempo de duración. Se utiliza más en el campo de la economía y de la física
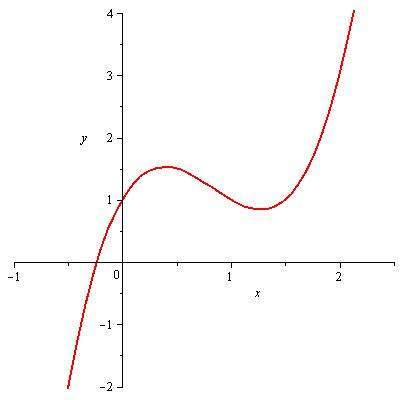
WEB GRAFIA: http://www.ecured.cu/index.php/Archivo:Funcion-cubica.jpg
Ejemplos
Grafique y analice las propiedades de la siguientes funciones
a) f(x) = 2x3 + 3x2 - 12x
Propiedades
2x3 + 3x2 - 12x = 0 x( 2x2 + 3x - 12) = 0 Extrayendo factor común x = 0 ( 2x2 + 3x + 12)= 0 Igualando a cero ambos factores y realizar la descomposición.
f(-1) = 2(-1)3 + 12 . (-1)2 + 2. (-1 )
b) F(x) = -x3 +8
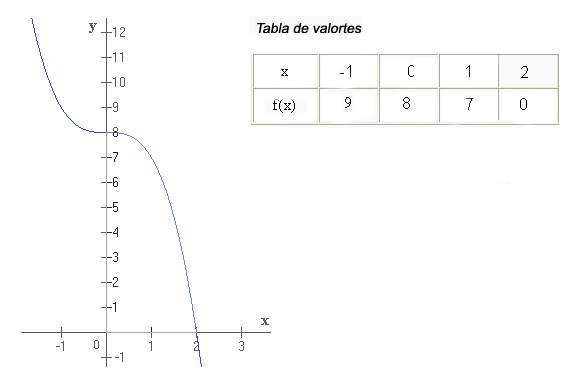
WEB GRAFIA: http://www.ecured.cu/index.php/Funci%C3%B3n_C%C3%BAbica

WEB GRAFIA: http://www.ecured.cu/index.php/Archivo:Funcion-cubica.jpg
Ejemplos
Grafique y analice las propiedades de la siguientes funciones
a) f(x) = 2x3 + 3x2 - 12x
Propiedades
- Dominio: El conjunto de los Reales
- Imagen: El conjunto de los Reales
- Ceros de la función:
2x3 + 3x2 - 12x = 0 x( 2x2 + 3x - 12) = 0 Extrayendo factor común x = 0 ( 2x2 + 3x + 12)= 0 Igualando a cero ambos factores y realizar la descomposición.
- Simetría: Demostrar que cumple f(-x)=-f(x).
f(-1) = 2(-1)3 + 12 . (-1)2 + 2. (-1 )
= 2.(-1) + 12 . 1 - 2
= -2 + 12 - 2
= 10 - 2
= 8
f(1) = 2(1)3 + 12 . (1)2 + 2. (1 ) = 2.(1) - 12 . 1 + 2
= 2 - 12 + 2
= -10 + 2
= -8
Como f(-1) = - f(1) por tanto la función es simétrica.- Continuidad: La función es continua en todo su dominio pues gráficamente se puede observar que no tiene ningún punto de discontinuidad.
- La función no tiene asuntotas.
- Para determinar los puntos donde la función corta el eje de la y
b) F(x) = -x3 +8

WEB GRAFIA: http://www.ecured.cu/index.php/Funci%C3%B3n_C%C3%BAbica
FUNCION CUADRATICA Y EJEMPLOS*
Son funciones polinómicas es de segundo grado, siendo su gráfica una parábola.
f(x) = ax² + bx +c
Representación gráfica de la parábola
Podemos construir una parábola a partir de estos puntos:
1. Vértice

Por el vértice pasa el eje de simetría de la parábola.
La ecuación del eje de simetría es:
2. Puntos de corte con el eje OX
En el eje de abscisas la segunda coordenada es cero, por lo que tendremos:
ax² + bx +c = 0
Resolviendo la ecuación podemos obtener:
Dos puntos de corte: (x1, 0) y (x2, 0) si b² − 4ac > 0
Un punto de corte: (x1, 0) si b² − 4ac = 0
Ningún punto de corte si b² − 4ac < 0
3. Punto de corte con el eje OY
En el eje de ordenadas la primera coordenada es cero, por lo que tendremos:
f(0) = a · 0² + b · 0 + c = c (0,c)
Representar la función f(x) = x² − 4x + 3.
1. Vértice
x v = − (−4) / 2 = 2 y v = 2² − 4· 2 + 3 = −1
V(2, −1)
2. Puntos de corte con el eje OX
x² − 4x + 3 = 0

(3, 0) (1, 0)
3. Punto de corte con el eje OY
(0, 3)

WEB GRAFIA: http://www.vitutor.com/fun/2/c_5.html
Ejercicios resueltos de la función cuadrática
1
Representa gráficamente la función cuadrática:
y = -x² + 4x - 3
1. Vértice
x v = - 4/ -2 = 2 y v = -2² + 4· 2 - 3 = -1 V(2, 1)
2. Puntos de corte con el eje OX.
x² - 4x + 3 = 0
 (3, 0) (1, 0)
(3, 0) (1, 0)
3. Punto de corte con el eje OY.
(0, -3)

WEB GRAFIA: http://www.vitutor.com/fun/2/e_c.html
FUNCION LINEAL Y EJEMPLOS*
La función lineal es del tipo:
y = mx + n
m es la pendiente de la recta.
La pendiente es la inclinación de la recta con respecto al eje de abscisas.
Dos rectas paralelas tienen la misma pendiente.

n es la ordenada en el origen y nos indica el punto de corte de la recta con el eje de ordenadas.

WEB GRAFIA: http://www.vitutor.net/1/funcion_lineal.html
Suscribirse a:
Comentarios (Atom)